Belastbarkeit: Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
;Knoten: Knoten im Seil (und an den Enden) reduzieren die Bruchlast des Seiles erheblich. Wieviel genau hängt natürlich vom Knoten ab und ist einer der Gründe warum in verschiedenen Situationen unterschiedliche Knoten verwendet werden, aber als Orientierung kann man sich den Wert 1/2 merken. Ein Knoten halbiert also die Bruchlast eines Seiles. | ;Knoten: Knoten im Seil (und an den Enden) reduzieren die Bruchlast des Seiles erheblich. Wieviel genau hängt natürlich vom Knoten ab und ist einer der Gründe warum in verschiedenen Situationen unterschiedliche Knoten verwendet werden, aber als Orientierung kann man sich den Wert 1/2 merken. Ein Knoten halbiert also die Bruchlast eines Seiles. | ||
;Geometrie: Die Bruchlast eines Seiles ist für den einfachsten Fall ausschlaggebend, nämlich dass das Seil senkrecht hängt, oben festgemacht ist und unten die Last dran hängt. In der Realität ist sowas selten der Fall, und unter bestimmten Umständen ist der Unterschied zwischen dieser und anderer Art der Belastung gewaltig. Zum einen baut man unter umständen bewusst oder unbewusst eine Art Flaschenzug dessen kraftverstärkende Wirkung sich natürlich auch negativ auf die Bruchlast auswirkt, zum anderen werden Seile häufig quer belastet (z.B. bei einer Seilbrücke oder -bahn) was die Bruchlast ebenfalls stark beeinflussen kann. | ;Geometrie: Die Bruchlast eines Seiles ist für den einfachsten Fall ausschlaggebend, nämlich dass das Seil senkrecht hängt, oben festgemacht ist und unten die Last dran hängt. In der Realität ist sowas selten der Fall, und unter bestimmten Umständen ist der Unterschied zwischen dieser und anderer Art der Belastung gewaltig. Zum einen baut man unter umständen bewusst oder unbewusst eine Art Flaschenzug dessen kraftverstärkende Wirkung sich natürlich auch negativ auf die Bruchlast auswirkt, zum anderen werden Seile häufig quer belastet (z.B. bei einer Seilbrücke oder -bahn) was die Bruchlast ebenfalls stark beeinflussen kann. | ||
| − | |||
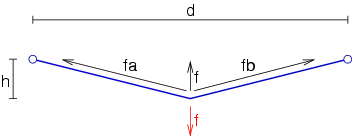
;Beispiel: [[Datei:Geometry.png|right]]Um das mal mit einem kleinen Beispiel zu belegen bauen wir eine Seilbahn von d=12 m Länge die h=0,5 m durchhängt. Daran hängen wir nun in der Mitte einen Pfadfinder mit 60 kg. Was muss das Seil nun aushalten? 60 kg? Bei weitem mehr! Das Problem ist nämlich (Achtung: Physik-Alarm!), dass das Seil die Kraft, die durch den Pfadfinder ausgeübt wird (etwa 600 N) mit einer Gegenkraft kompensieren muss, und diese muss sich aus zwei Kräften entlang der beiden Seilhälften zusammensetzen. Da diese zwischen sich einen sehr flachen Winkel einnehmen, sind diese Kräfte extrem groß. Zur genauen Berechnung benötigt man den Sinus, aber als Annäherung kann man die auftretende Kraft mal die Halbe Seillänge nehmen und durch die doppelte Durchhangshöhe teilen. In unserem Fall muß das Seil also 3600 N statt der 600 N aushalten. Zusammen mit dem Problem dass die Knoten am Ende die Belastbarkeit halbieren sind wir bei etwa 7000 N, mit einigem Spielraum (wir wollen ja nichts riskieren) nehmen wir ein Seil mit über 10 kN Bruchlast. Die ganze Sache wird um so extremer je weniger das Seil durchhängt, also um so flacher der Winkel zwischen den beiden Seilhälften ist. In anderen Fällen treten ähnliche Effekte auf und die Berechnungen sind oft noch komplizierter, aber zumindestens diesen Fall ein waagrecht gespanntes Seil (oder auch einen Balken!) in der Mitte unter einem kleinen Winkel quer zu belasten sollte man erkennen und vermeiden. | ;Beispiel: [[Datei:Geometry.png|right]]Um das mal mit einem kleinen Beispiel zu belegen bauen wir eine Seilbahn von d=12 m Länge die h=0,5 m durchhängt. Daran hängen wir nun in der Mitte einen Pfadfinder mit 60 kg. Was muss das Seil nun aushalten? 60 kg? Bei weitem mehr! Das Problem ist nämlich (Achtung: Physik-Alarm!), dass das Seil die Kraft, die durch den Pfadfinder ausgeübt wird (etwa 600 N) mit einer Gegenkraft kompensieren muss, und diese muss sich aus zwei Kräften entlang der beiden Seilhälften zusammensetzen. Da diese zwischen sich einen sehr flachen Winkel einnehmen, sind diese Kräfte extrem groß. Zur genauen Berechnung benötigt man den Sinus, aber als Annäherung kann man die auftretende Kraft mal die Halbe Seillänge nehmen und durch die doppelte Durchhangshöhe teilen. In unserem Fall muß das Seil also 3600 N statt der 600 N aushalten. Zusammen mit dem Problem dass die Knoten am Ende die Belastbarkeit halbieren sind wir bei etwa 7000 N, mit einigem Spielraum (wir wollen ja nichts riskieren) nehmen wir ein Seil mit über 10 kN Bruchlast. Die ganze Sache wird um so extremer je weniger das Seil durchhängt, also um so flacher der Winkel zwischen den beiden Seilhälften ist. In anderen Fällen treten ähnliche Effekte auf und die Berechnungen sind oft noch komplizierter, aber zumindestens diesen Fall ein waagrecht gespanntes Seil (oder auch einen Balken!) in der Mitte unter einem kleinen Winkel quer zu belasten sollte man erkennen und vermeiden. | ||
| − | + | ==Autor: Robert L.== | |
| − | |||
| − | =Autor: Robert L.= | ||
Quelle: http://www.schlauesbuch.de | Quelle: http://www.schlauesbuch.de | ||
Aktuelle Version vom 1. April 2021, 18:31 Uhr
Bei der Überlegung welches Seil für einen bestimmten Zweck verwendet werden soll, spielt sicherlich die Belastbarkeit eine große Rolle. Hierbei sollten wir zunächst einmal stark zwischen der Belastbarkeit im Sinne von einem Abnützen über die Dauer der Belastung, und einer kurzen Einzelbelastung unterscheiden. Der erste Fall ist in erster Linie vom Material des Seils und den Umweltbedingungen (Feuchtigkeit, UV, Kälte, Schmutz...) abhängig, sowie davon, ob sich das Seil bewegt (also auch scheuert) oder nicht. Leider lässt sich für diesen Fall nur wenig sagen ausser: regelmässig kontrollieren, im Zweifelsfall austauschen und mit reichlich Spielraum dimensionieren.
Über die Einzelbelastung lässt sich schon mehr sagen, hier gibt es einen Wert der für die meisten Seile vom Hersteller angegeben wird, die Bruchlast. Diese ist ein Richtwert, der angibt welche Belastung das Seil unter bestimmten Normbedingungen aushält. Die Bruchlast wird beeinflusst vom Material des Seils und seinem Durchmesser (doppelt so dick = 4 mal soviel Bruchlast). Leider ist diese Bruchlast nur ein Richtwert, der nicht einfach so verwendet werden kann, da es sehr viele Faktoren gibt, die die Bruchlast noch beeinflussen:
- Belastungstyp
- Die Bruchlast gilt für ein statisches System, also eines in dem keine Bewegung stattfindet. Insbesondere ist es keine Fallbelastung! Eine Bruchlast von einer Tonne bedeutet also, dass das Seil theoretisch eine Tonne halten kann, nicht aber auffangen wenn diese gefallen ist.
- Knoten
- Knoten im Seil (und an den Enden) reduzieren die Bruchlast des Seiles erheblich. Wieviel genau hängt natürlich vom Knoten ab und ist einer der Gründe warum in verschiedenen Situationen unterschiedliche Knoten verwendet werden, aber als Orientierung kann man sich den Wert 1/2 merken. Ein Knoten halbiert also die Bruchlast eines Seiles.
- Geometrie
- Die Bruchlast eines Seiles ist für den einfachsten Fall ausschlaggebend, nämlich dass das Seil senkrecht hängt, oben festgemacht ist und unten die Last dran hängt. In der Realität ist sowas selten der Fall, und unter bestimmten Umständen ist der Unterschied zwischen dieser und anderer Art der Belastung gewaltig. Zum einen baut man unter umständen bewusst oder unbewusst eine Art Flaschenzug dessen kraftverstärkende Wirkung sich natürlich auch negativ auf die Bruchlast auswirkt, zum anderen werden Seile häufig quer belastet (z.B. bei einer Seilbrücke oder -bahn) was die Bruchlast ebenfalls stark beeinflussen kann.
- Beispiel
- Um das mal mit einem kleinen Beispiel zu belegen bauen wir eine Seilbahn von d=12 m Länge die h=0,5 m durchhängt. Daran hängen wir nun in der Mitte einen Pfadfinder mit 60 kg. Was muss das Seil nun aushalten? 60 kg? Bei weitem mehr! Das Problem ist nämlich (Achtung: Physik-Alarm!), dass das Seil die Kraft, die durch den Pfadfinder ausgeübt wird (etwa 600 N) mit einer Gegenkraft kompensieren muss, und diese muss sich aus zwei Kräften entlang der beiden Seilhälften zusammensetzen. Da diese zwischen sich einen sehr flachen Winkel einnehmen, sind diese Kräfte extrem groß. Zur genauen Berechnung benötigt man den Sinus, aber als Annäherung kann man die auftretende Kraft mal die Halbe Seillänge nehmen und durch die doppelte Durchhangshöhe teilen. In unserem Fall muß das Seil also 3600 N statt der 600 N aushalten. Zusammen mit dem Problem dass die Knoten am Ende die Belastbarkeit halbieren sind wir bei etwa 7000 N, mit einigem Spielraum (wir wollen ja nichts riskieren) nehmen wir ein Seil mit über 10 kN Bruchlast. Die ganze Sache wird um so extremer je weniger das Seil durchhängt, also um so flacher der Winkel zwischen den beiden Seilhälften ist. In anderen Fällen treten ähnliche Effekte auf und die Berechnungen sind oft noch komplizierter, aber zumindestens diesen Fall ein waagrecht gespanntes Seil (oder auch einen Balken!) in der Mitte unter einem kleinen Winkel quer zu belasten sollte man erkennen und vermeiden.
Autor: Robert L.
Quelle: http://www.schlauesbuch.de